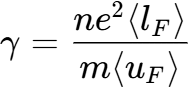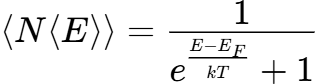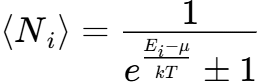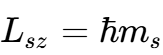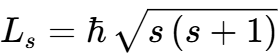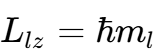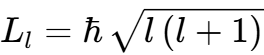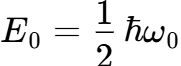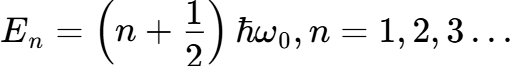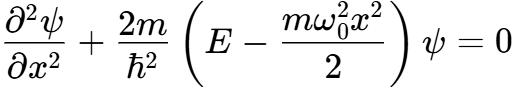Результаты поиска: формул(ы)
3.6.598. Электрическая проводимость металла, согласно квантовой теории электропроводности металлов
Просм.: 158
·
Сохранений: 0
·
Ком.: 0
3.6.596. Распределение Ферми-Дирака по энергиям для свободных электронов в металле
Просм.: 145
·
Сохранений: 0
·
Ком.: 0
3.6.593. Спин (собственный механический момент импульса) электрона
Просм.: 146
·
Сохранений: 0
·
Ком.: 0
3.6.591. Момент импульса (механический орбитальный момент) электрона
Просм.: 153
·
Сохранений: 0
·
Ком.: 0
3.6.589. Собственное значение энергии гармонического осциллятора
Просм.: 144
·
Сохранений: 0
·
Ком.: 0
3.6.588. Уравнение Шредингера для линейного гармонического осциллятора в квантовой механике
Просм.: 156
·
Сохранений: 0
·
Ком.: 0
Формула